Astronomy Tuesday: Living in a Hologram

It's been a while since I've written about astronomy, so I figured I should get back on it. I just got back from a public lecture given by Leonard Susskind of Stanford University which was this year's Sackler Public Lecture hosted by the Canadian Institute for Theoretical Astrophysics (CITA). Susskind is one of the great living physicists, and is certainly one of the best public lecturers I have ever seen. He has a Feynman-esque quality to his talking, and it's not just the New York accent. The ideas he presented flowed beautifully into one another, and though all his diagrams were obviously created in MS Paint, I never once felt like I was missing the point.

His lecture this evening was about the Holographic Universe, which doesn't have anything to do with holograms like in Star Trek, but instead means that all the 3-dimensional information in the universe can be represented on a 2-dimensional surface, sort of like how the 2D surface of a hologram shows 3D features. (Image from Crispers Handmade Holographic Images page)

The story began with black holes, which are one of my favourite things to talk about (and are, in fact, the area of my research, which I might talk about someday). These objects are essentially points of infinite density that have an imaginary boundary called the "event horizon" which is the point beyond which even light cannot escape the gravitational field of the black hole. That is, you'd need to be traveling faster than the speed of light in order to escape its gravitational pull. Susskind used a nice analogy with fish and a whirlpool in a lake, where past the event horizon, it is impossible for the fish to swim fast enough to escape the whirlpool. The following diagram (taken from AnsweringGenenis.com, which is a pretty good article if you ignore the God stuff) shows the basic idea:

It got a little more complicated after that. One of the most fundamental laws of physics, he says, is that information cannot be lost to the Universe. Even when you delete a little piece of information off your hard drive, for example, that information is transformed into heat which goes out into the environment. The problem with this, however, is that when something falls into a black hole, all information about that object is lost to the outside world, since even the light from that object can't escape the black hole's event horizon.

The next issue has to do with entropy. Entropy is a quantity which more or less describes the amount of disorder in a system. In thermodynamics, it's officially defined as the "unavailability of a system's thermal energy for conversion into mechanical work" (Google Dictionary). A commonly-used example is gas in a box. If you have one side of a box that has a bunch of gas molecules in it, and the other side is a vacuum, and you remove the barrier, the gas will go from one side of the box to the other and eventually mix more or less evenly. (Diagram from Principia Cybernetica Net)

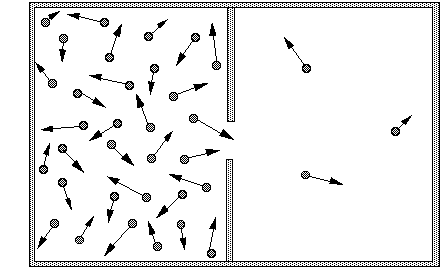
The idea is that it goes from a state of higher order, with the gas molecules on one side of the box, to a state of less order, with the gas molecules floating all around the box. With a black hole, however, you'd expect the disorder to decrease if some gas fell in past the event horizon because the gas would become part of the black hole, which can be described simply by the size of its event horizon. However, a very smart guy named Jacob Bekenstein used some fancy physics to show that black holes actually have very high entropy, and that it can, in fact, be explained by the following elegant formula:

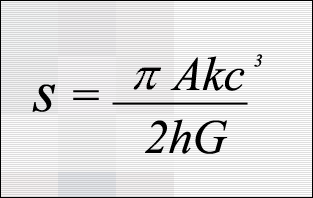
I'm not going to explain the entire formula, but the important parts are the S on the left hand side and the A on the right hand side. The former represents entropy, and the latter represents the area of the event horizon of the black hole. This means that the entropy of the black hole is directly proportional to its area, and not its volume, as one might expect. It's a mapping of 3D information onto a 2D surface... Just like a hologram!

This still leaves the loss of information problem. However, Susskind and other people then used crazy kinds of string theory (like there's any other kind) to show that deformations on the surface of the event horizon could describe (if you could measure them) the properties of the matter that has fallen in to the black hole. So just like a hologram uses a 2D surface to encode information about 3D objects, the 2D surface of a black hole would encode the information about stuff that's fallen into it. (Image of a hologram from Wikipedia)

Susskind also said that you could think of the Universe the same way... that information within a certain volume can be encoded on the boundary of this volume. This is called the Holographic Principle. This means that the information contained within the Universe could be described by information encoded on its boundary, that is, its event horizon. Essentially, we're living in a hologram!

If you want to learn more about Leonard Susskind's work, he's written a couple of popular science books: The Cosmic Landscape, where he talks about string theory, and The Black Hole War, where he talks about information and matter falling into black holes. I haven't read either, but I have it on good authority that they're both really good, so go check them out!